BÀI LÀM CỦA TÔI TRONG PSW_4

PSW Leave a comment

Cho tam giác ABC có M thuộc miền trong của tam giác. Các đường thẳng AM;BM;CM cắt đường tròn (ABC) tại A′,B′,C′. Gọi r và r′ lần lượt là bán kính đường tròn nội tiếp các tam giác ABC và A′B′C′, còn R là bán kính đường tròn ngoại tiếp tam giác ABC
Chứng minh rằng: 4rr'\leq R^{2}-OM^{2}

Lời giải:

Ta có: MA.MA'=R^{2}-OM^{2}

Ta có BĐT sau:

\dfrac{MA.MB.MC}{MA.MA'}=\dfrac{MA.MB.MC}{R^{2}-OM^{2}}\geq 2r

Áp dụng tương tự cho tam giác A’B’C’

\Rightarrow \dfrac{MA'.MB'.MC'}{R^{2}-OM^{2}}\geq 2r'\Rightarrow 4rr'\leq \dfrac{MA.MB.MC}{R^{2}-OM^{2}}.\dfrac{MA'.MB'.MC'}{R^{2}-OM^{2}}

=\dfrac{(MA.MA')(MB.MB')(MC.MC')}{(R^{2}-OM^{2})^{2}}=\dfrac{(R^{2}-OM^{{2}})^{{3}}}{(R^{{2}}-OM^{{2}})^{{2}}}=R^{{2}}-OM^{{2}} (đpcm)

BÀI LÀM CỦA TÔI TRONG PSW_3

PSW Leave a comment

Cho n là số nguyên dương. Tìm giá trị lớn nhất của các biểu thức sau:

A=\dfrac{n}{(1,1)^{n}};B=\dfrac{n^{2}}{(1,1)^{n}}

Lời giải:

Đặt: f(n)=\dfrac{n}{(1,1)^{n}}

g(n)=\dfrac{n^{2}}{(1,1)^{n}}

+) Đối với f(n): Dùng phép biến đổi tương đương, ta chứng minh được:

f(n+1)>f(n) với \forall n=1,2,...,9

f(n)>f(n+1) với \forall n=11,12,13,...

Trong đó f(10)=f(11)=\dfrac{10^{11}}{11^{10}}. Vậy f(10)>f(9)>f(8)>...>f(1) ;

f(11)>f(12)>f(13)>...

Từ đó \Rightarrow f(n) đạt GTLN=\dfrac{10^{11}}{11^{10}} khi n=10 hoặc n=11

++) Đối với g(n) : Dùng phép biến đổi tương đương, ta chứng minh được:

g(n+1)>g(n), với \forall n=1,2,3,...,20

g(n)>g(n+1), với \forall n=21,22,23,...

Vậy: g(21)>g(20)>g(19)>...>f(1)

g(21)>g(22)>g(23)>....

Tứ đó suy ra g(n) đạt GTLN=g(21)=\dfrac{441}{(1,1)^{21}} khi n=21 

BÀI LÀM CỦA TÔI TRONG PSW_2

PSW 1 Comment

Cho tam giác ABC vuông tại A, vẽ đường cao AH. Gọi (O) là đường tròn ngoại tiếp tam giác AHC. Trên cung nhỏ AH của đường tròn (O) lấy điểm M bất kì khác A.Trên tiếp tuyến tại M của đường tròn (O) lấy hai điểm Dvà E sao cho BD=BE=BA. Đường thẳng BM cắt đường tròn (O) tại điểm thứ hai N.
a) Chứng minh rằng tứ giác BDNE nội tiếp một đường tròn.
b) Chứng minh đường tròn ngoại tiếp tứ giác BDNE và đường tròn (O) tiếp xúc với nhau.

 Lời giải:

Ảnh

a) Xét \Delta BAM và \Delta BNA có:

\widehat{ABN} chung

\widehat{BAN}=\widehat{BNA}

\Rightarrow \Delta BAM \sim \Delta BNA (g.g)

\Rightarrow \dfrac{BA}{BM}=\dfrac{BN}{BA}\Rightarrow BA^{2}=BM.BN mà BD=BA

\Rightarrow BD^{2}=BM.BN

\Rightarrow \dfrac{BD}{BM}=\dfrac{BN}{BD} mà \widehat{DBN} chung

\Rightarrow \Delta BMD\sim \Delta BDN \Rightarrow \widehat{BND}=\widehat{BDM} (1)

Lại có \Delta BDE cân (BD=BE)

\Rightarrow \widehat{BDM}=\widehat{BED} (2)

Từ (1) và (2) \Rightarrow \widehat{BND}=\widehat{BED}

Vậy tứ giác BDNE nội tiếp đường tròn

b) Gọi O’ là tâm đường tròn ngoại tiếp tứ giác BDNE

\Rightarrow \widehat{BO'N}=2\widehat{BEN} \Rightarrow \widehat{BEN}=\widehat{BED}+\widehat{DNE}=\widehat{BDE}+\widehat{DBN}

Lại có: \widehat{DMN}=\widehat{BDE}+\widehat{DBN}

\Rightarrow \widehat{BEN}=\widehat{DMN}\Rightarrow \widehat{BO'N}=2\widehat{DMN}\Rightarrow BNO'=\dfrac{180^{0}-2\widehat{DMN}}{2}=90^{0}-\widehat{DMN} (3)

Xét (O) ta có: \widehat{MON}=2\widehat{DMN}

\Rightarrow \widehat{BNO}=90^{0}-\widehat{DMN} (4)

Từ (3) và (4) \Rightarrow \widehat{BNO'}=BNO

\Rightarrow N,O,O’ thẳng hàng

Vậy đường tròn ngoại tiếp tứ giác BDNE và (O) tiếp xúc nhau

🙂

Bài làm của tôi trong PSW_1

PSW 1 Comment

Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAC. Với M thuộc miền tứ giác ABCD, MG cắt mặt bên của hình chóp tại N. Hãy tìm giá trị lớn nhất, nhỏ nhất của
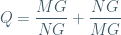
Q = \dfrac{MG}{NG}+\dfrac{NG}{MG}

Giả sử O là giao điểm 2 đường chéo hình bình hành ABCD

MO cắt AD,CD lần lượt tại E và F ; MG cắt SF tại N là giao của MG và mặt bên của hình chóp

+) GTNN:

Áp dụng bất đẳng thức cauchy: 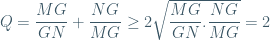Q=\dfrac{MG}{GN}+\dfrac{NG}{MG}\geq 2\sqrt{\dfrac{MG}{GN}.\dfrac{NG}{MG}}=2

Vậy Q đạt GTNN khi 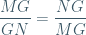\dfrac{MG}{GN}=\dfrac{NG}{MG} hay MG=GN

Tam giác SEF: ta kẻ từ N đường thẳng song song với EF cắt SO tại K

Ta có: \dfrac{KG}{GO}=\dfrac{GN}{MG}=1\Rightarrow SK=KG=GO=\dfrac{1}{3}SO\Rightarrow \dfrac{KN}{OF}=\dfrac{SK}{SO}=\dfrac{1}{3}\Rightarrow KN=\dfrac{OF}{3}

Vậy M là tập hợp những điểm nằm trên cạnh hình bình hành A’B’C’D’ có các cạnh song song với các cạnh của hình bình hành ABCD và có cạnh bằng \dfrac{1}{3} hình bình hành ABCD

+) GTLN

Giả sử tam giác SEF cố định (1)

Điểm M chạy trên EF ta tìm GTLN của Q

Tam giác MNF: kẻ từ G đường thẳng song song với SF cắt OF tại H và từ G kẻ đường thẳng song song với SE cắt OE tại U

\Rightarrow Q=\dfrac{MG}{NG}+\dfrac{GN}{MG}=\dfrac{MH}{HF}+\dfrac{HF}{MH}(2)

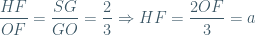Ta lại có: \dfrac{HF}{OF}=\dfrac{SG}{GO}=\dfrac{2}{3}\Rightarrow HF=\dfrac{2OF}{3}=a( không đổi)

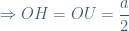
\Rightarrow OH=OU=\dfrac{a}{2}

Ta luôn có: 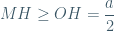MH\geq OH=\dfrac{a}{2}(do M ở cùng phía với OE còn nếu ở cùng phía với OF thì ngược lại);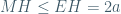MH\leq EH=2a

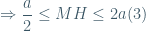
\Rightarrow \dfrac{a}{2}\leq MH\leq 2a(3)

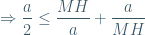
\Rightarrow \dfrac{a}{2}\leq \dfrac{MH}{a}+\dfrac{a}{MH}

Đặt MH=x, xét hàm số f(x)=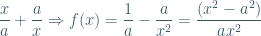\dfrac{x}{a}+\dfrac{a}{x}\Rightarrow f(x)=\dfrac{1}{a}-\dfrac{a}{x^{2}}=\dfrac{(x^{2}-a^{2})}{ax^{2}}

Từ 3 ta được:

Nếu 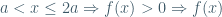a<x\leq 2a\Rightarrow f(x)>0 \Rightarrow f(x)đồng biến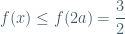 f(x)\leq f(2a)=\dfrac{3}{2}

Nếu 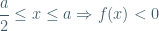\dfrac{a}{2}\leq x\leq a\Rightarrow f(x)<0 (nghịch biến) \Rightarrow f(x)\leq f(\dfrac{a}{2})=\dfrac{3}{2}

Vậy Q đạt GTLN khi MH đạt GTLN =\dfrac{3}{2} khi M trùng E hoặc trùng O

Chứng minh tương tự cho giả thiết tam giác SEF quay quanh cạnh SO ta đều được GTLN là \dfrac{3}{2}

Vậy tập hợp các điểm M để Q đạt GTLN là các điểm nằm trên cạnh hình bình hành ABCD và trùng với tâm O của ABCD với GTLN của Q là \dfrac{3}{2}

🙂

BƯỚM ĐƠN BƯỚM KÉP -ĐỊNH LÝ HARUKI

Uncategorized 1 Comment

Trong thế giới toán học, đâu phải chỉ có sự ngự trị của các con số. Trong mục này các bạn sẽ thấy chúng – những con số – chỉ là phần tĩnh của những thực thể sống. Đó là cả 1 phiên bản đẹp của thế giới động vật đầy sức sống. Nắm được cái tĩnh trong động là 1 việc khó. Nhưng nắm được cái động trong tĩnh lại là 1 công việc đầy thú vị………….

Bài toán bướm đơn:
PQ là 1 dây cung của đường tròn (O); AB,CD là 2 dây cung của đường tròn đó và cùng đi qua trung điểm Ecủa dây cung PQ; AD,BC cắt PQ tại M,N tương ứng. Khi đó MN cũng nhận E làm trung điểm.

Ảnh

Hình vẽ trên là 1 minh họa sống động cho định lý này: các bạn có thể thấy rõ phần gạch chéo là hình ảnh của 1 chú bướm đang xoè cánh bay. Và nếu như nối AC,BD cắt PQ thì ta lại nhận được 1 chú bướm khác.

Chứng minh định lý này như thế nào? Có rất nhiều cách: chẳng hạn lấy C′D′ đối xứng với CD qua trung trực của PQ rồi chứng mình tam giác C’EM và CEN bằng nhau. Hoặc chứng minh trực tiếp tam giác OMN cân.

Ảnh

Hầu hết những cách chứng minh hình học đều rất thú vị (không chỉ với những bài toán hình học mà ngay cả với những bài toán đại số cũng thế). Tuy nhiên dưới đây chúng ta sẽ làm quen với 1 chứng minh mang tính đại số hơn, bởi vì những hiệu quả của nó đem lại là rất đáng quan tâm.

Chứng minh của định lý bướm đơn: Gọi M’,M” (tương ứng N’,N”) là hình chiếu vuông góc của M (tương ứng N) trên AB,CD. Lần lượt có:

  • \dfrac{AM.MD}{CN.ND}=\dfrac{EM^{2}}{EN^{2}}
  • x=PM,x'=PM',y=MN,y'=M'N',z=NQ,z'=N'Q

Lập luận như trên ta có: \dfrac{y(x'-x)}{(z-z')y'}=\dfrac{x(y+z)}{(x'+y')z'} và từ đó x.y'.z=z'.y.z'

Bây giờ nhờ định lý Haruki ta thu được chứng minh khá đơn giản cho bài toán bướm kép:

Bài toán bướm kép:Các dây cung đuợc bố trí như hình vẽ.Giả sử PF=P'F',PG=P'G',PH=P'H'
Dùng định lý Haruki ta có

  • \dfrac{PE.FP'}{EF}=\dfrac{PG.HP'}{GH}
  • \dfrac{P'E'.F'P}{E'F'}=\dfrac{P'G'.H'P}{G'H'}

Từ đó suy ra PE=P'E'

Hệ thức Ơ-le

Uncategorized Leave a comment

Ảnh

Gọi O,I là tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC,M là giao của phân giác góc B với (O)
Kẻ đường kính qua O,I cắt (O) tại 2 điểm là N,P
Có R^{2}-OI^{2}=(R+OI)(R-OI)=(ON+OI)(OP-OI)=IN.IP
Mà IN.IP=IB.IM(cm bằng tam giác đồng dạng)
Nên BI.IM=IN.IP=R^{2}-OI^{2}=R^{2}-d^{2}(1)
Tam giác ICM cân tại M(vì \widehat{CIM} = \widehat{ICM} =\dfrac{B+C}{2})\Rightarrow MC=MI
kẻ đường kính MK của (O) và kẻ ID \perp BC ta cm đc 2 tam giác MKC và IBD đồng dạng nhau
\Rightarrow \dfrac{MK}{MC}=\dfrac{IB}{ID}
Do MK=2R,ID=r,MC=MI nên 2Rr=MK.ID=IB.MC=IB.IM=R^{2}-d^{2}(2)
Từ (1) và (2)\Rightarrow dpcm

😆